Table of Contents

• What is Amplitude?
• Amplitude Quantization Error
• Challenges Faced in Amplitude Quantization Error
• Conclusion

What is Amplitude?

Amplitude is the maximum displacement or distance moved by a point on a vibrating body or wave measured from its equilibrium position. It is equal to one-half the length of the vibration path.  Ripples in water, sound traveling in air, and coordinated vibrations of objects are examples of waves you have probably encountered in your life. A good way to visualize a wave is to insert the end of a pencil into a container of still water. The surface of the water is disturbed, producing ripples, or waves.

You may also like to read:

1. Festoon Cable System
2. Vibration Sensors: An Overview

Electromagnetic waves, such as light, radio waves, microwaves, and X-rays, are special waves that do not require a medium for propagation. We cannot see or hear these waves, but they exist in nature and in many of the products we use every day.

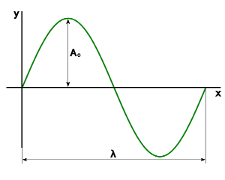
Regardless of the kind, every wave has an amplitude. Amplitude is the maximum displacement of points on a wave, which you can think of as the degree or intensity of change. This maximum displacement is measured from the equilibrium position. The following picture shows a diagram of a sine wave. The diagram shows amplitude and wavelength, which is the distance between two successive like points on a wave. Wavelength is like the distance between two adjacent peaks or two adjacent valleys.  Stated another way, wavelength is the time required to complete one full cycle of the wave.

The equilibrium position is the straight line represented by the x-axis. It represents the shape of the medium when there is no wave, or when the water is still and undisturbed in the case of ripples in water. This helps us see another way to state the definition of amplitude, which is the vertical distance from a peak to the equilibrium position or from the equilibrium position to a valley. Amplitude is used to describe the peak value of such quantities as the level of sound waves, and power and voltage in electrical and electronic systems.

Amplitude Quantization Error

Quantization error is caused during the acquisition of data.  It is synonymous with rounding error. In order to explain this, a real-time signal has been artificially modified to an extreme to show the difference between a signal sampled with adequate amplitude resolution and the same signal sampled with insufficient amplitude resolution. Also, this example was taken into the frequency domain to demonstrate how quantization error can affect the spectrum of the signal.

Challenge faced in Amplitude Quantization Error

Amplitude Quantization Error is typically caused by not having sufficient amplitude resolution to accurately capture the exact amplitude of the signal. With modern ADCs using 24 or even 16-bit resolution, this is not typically a problem, however, measurement systems with fewer bits of amplitude resolution can compromise the data.

The cause of this insufficient resolution is based on the sampling of the level of a signal, or in other words, having too few bits to accurately define the signal level during the sampling process. Typically analog to digital converters have a specified voltage range that they can accept. The range is ±10 Volts. The ADC’s in these systems are 24-bit which means the total range of 20 Volts (±10 Volts) is 16777216 (224) different levels. This should be more than a sufficient number of levels to adequately define the signal level from most transducers. To demonstrate this, a signal is sampled with adequate amplitude resolution (Figure 1).

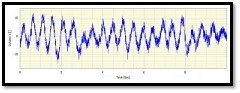
Figure 1: Data sampled with adequate
amplitude resolution

However, under rare circumstances, if the transducer used has a very low sensitivity (e.g. 1µV/EU) and the system gain is not adjusted to using the full ADC range, this can lead to the amplitude not having an adequate resolution to accurately describe the signal. If only ±1 V or less of the ±10 V available of the ADC range is used there are far fewer levels that can be used to define the signal level.

Now the same data artificially modified introducing an extreme amount of rounding error is shown in Figure 2. The levels of approximately -15 EU to +12.5 EU have been rounded to quantized levels of -12, -8, -4, 0, 4, 8, and 12.  This, of course, is an exaggeration, but it becomes visually apparent that there is a problem with this data.

What does this mean about the spectrum of a measurement taken with inadequate amplitude resolution? I have processed both these signals using the RMS Auto spectrum analysis tool and overlayed the results (See Figure 3). At first thought, one might expect to see this quantization carried over into the spectrum. This is not the case due to how the amplitude of each of the frequency bins is calculated in the FFT calculations.  A significantly higher noise floor is apparent for the signal with the quantization error. This can potentially mask peaks in the spectrum at or below this noise floor

Taking a closer look, it appears there is a discrepancy in the amplitudes of the two signals (Figure 4). Further investigation into this was to bandpass the time signals (w/o quantization error and w/ quantization error) around the frequencies of the 2 dominant peaks in the spectral data (2 Hz and 58 Hz). The RMS values of each of these 2 bandpass time signals were calculated and there is very close agreement to those values in the spectral calculations

Conclusion

There are two quick solutions to the problem of amplitude quantization error. The first is to use the appropriate transducer for the range of levels measured with the transducer and the second is to apply gain to the signal to use at least 50% of the available ADC range of the measurement system. In most cases, one or both suggestions used together will resolve the situation of inadequate amplitude resolution.

Frequently Asked Questions (FAQs)